Observemos que todos los valores obtenidos son números primos ¿Será cierto que para cualquier entero x el valor que se obtiene es un número primo?Responderemos esta pregunta más adelante. Veamos otro problema de ejemplo.
Considera un triángulo rectángulo isósceles con catetos iguales a 1 sobre la hipotenusa de éste se levanta un segundo triángulo de cateto igual a 1, sobre la hipotenusa de este nuevo triángulo se levanta un tercer triángulo rectángulo y así sucesivamente. Encuentra la longitud de la hipotenusa del triángulo número 1998.
Usando el teorema de Pitágoras obtenemos que la primera hipotenusa vale √2, la tercera vale √3, la cuarta vale √4. Si este patrón continuara, obtendríamos que la hipotenusa del triángulo 1998 sería √1999. Pero, ¿podemos asegurar que este patrón realmente continúa?
El método de inducción matemática.
En muchos problemas necesitamos demostrar que una propiedad que depende de un número entero n se cumple para todos los enteros positivos. La técnica canónica que usaremos para lograr este objetivo se denomina inducción matemática.
En su forma simple, este método consta de dos etapas:
1.Se verifica que la propiedad se cumple para un valor inicial ( n=1).
2. Se demuestra que si la propiedad se cumple para algún entero k, entonces se cumple para el siguiente (k +1).
Una vez verificados esos 2 requisitos, podemos verificar que la propiedad se cumple para n = 1, 2,3,....
Veamos un ejemplo práctico antes de analizar porque funciona el método. En el problema del triángulo, queremos comprobar la propiedad
La hipotenusadel triángulo n es √(n +1).
Notemos que la propiedad depende de un y sólo un número entero, el valor de n.Esto es un indicador de que el método de inducción matemática podría ser apropiado.
La primera etapa pide mostrar que la propiedad se cumple para n=1, es decir , que la hipotenusa del primer triángulo es √2, lo cual es cierto en virtud del teorema de Pitágoras.
En la segunda etapa, imaginamos que ya sabemos que la propiedad se cumple para algún valor de k ( o sea la hipotenusa del triángulo k es √(k +1) ).Queremos probar que la propiedad también se cumple para k +1 (o sea, la hipotenusa del triángulo k+1 es √(k +2)).
Para calcular la hipotenusa del triángulo k +1 aplicamos el teorema de Pitágoras. Uno de sus catetos es 1, y el otro es la hipotenusa del triangulo anterior, el cual estamos suponiendo que vale √(k +1). Entonces
Comprobamos que si la propiedad se cumple para un entero k, se cumple para k +1 . Entonces la inducción matemática nos garantiza que la propiedad siempre se cumple, y ya somos capaces de asegurar que la hipotenusa del triangulo 1998 es √1999.
¿Por qué funciona el método?
Este proceso puede compararse a una escalera, donde la primera etapa nos da el primer peldaño, y la segunda etapa construye nuevos peldaños a partir de los anteriores. La primera etapa prueba que la propiedad se cumple para n=1, dándonos un punto de partida. La segunda etapa dice que si sabemos que la propiedad se cumple para algún entero, se cumple para el siguiente.¡ Pero la primera etapa nos dice que la propiedad se cumple para n =1! Entonces podemos asegurar que la propiedad se cumple para el siguiente entero, es decir n =2. Como la propiedad se cumple para n=2, la segunda etapa nos dice que se cumple para el siguiente n =3.Como ahora ya sabemos que se cumple para n=3 ,la segunda etapa nos dice que la propiedad se cumple para n =4, y así sucesivamente.
Esto basta para asegurar que la propiedad se cumple para n= 1,2,3,4... ya que no importa que número escojamos, en algún momento la escalera “alcanza” ese número.
Variantes del método de inducción.
El análisis del método de inducción sugiere algunas variantes. Por ejemplo, en la primera etapa , el valor inicial no necesariamente tiene que ser 1. Si en la primera etapa probamos (por ejemplo) que la propiedad se cumple para n =10 , el método de inducción nos garantiza que la propiedad se cumple únicamente para n= 11,12... y si probásemos que la propiedad se cumple para n = -3, el método de inducción nos garantiza que la propiedad se cumple para n = -3,-2,-1, 0, 1,2,... Sin embargo, en la mayoría de los problemas el paso inicial es n =0 o n = 1.
La segunda etapa también es susceptible de modificación. Un ejemplo sería probar que si la propiedad se cumple para algún entero k , se cumple para k +2 . En este caso suponiendo que el valor inicial fuese n =1, habríamos que la propiedad se cumple para n = 1, 3,,5,7... ( Cerciorarse de este hecho). Sin embargo, las modificaciones a la segunda etapa son bastante raras, y con frecuencia pueden evitarse escogiendo adecuadamente las variables de la inducción.
Importancia de las dos etapas.
Si bien es cierta que la segunda etapa es la que “demuestra” que la propiedad se cumple, la primera tiene una importancia fundamental. Un error común es dar por sentada la primera parte del método y comprobar únicamente la segunda. Este es un error que se debe evitar, pues es necesario tener un punto inicial para que la inducción pueda funcionar. Consideremos el siguiente ejemplo.
En el problema del triángulo, imaginemos que equivocadamente hubiéramos notado que la hipotenusa del triangulo n era √(n-1).
En la segunda etapa suponemos que la propiedad se cumple para un k e intentamos probar que también se cumple para un k +1. Usando el teorema de Pitágoras:
Y concluimos que la hipotenusa del triangulo n es ! √(n-1) en vez de √(n+1)!
El error provino de omitir la primera etapa, que es la que nos provee de una base verdadera para que la segunda etapa construya una escalera de verdades.
Analicemos ahora el problema del polinomio. Después de probar los primeros 20 números obtenemos siempre números primos ( esto equivaldría a realizar la primera etapa), sin embargo, como nos es difícil probar la segunda parte, nos vemos tentados a decir “ después de hacer muchos casos”, concluimos que el polinomio siempre devuelve números primos”. Este es un error aún más grande que el anterior ,pues
P (41) = 412 +41 +41 = 41 (41 +1+ 1)= 41× 43
Y tenemos que el polinomio no siempre genera números primos. La moraleja es que si algún patrón parece repetirse de manera constante, es bueno señalarlo, pero hasta no realizar ambos pasos de la inducción no podemos garantizar que la propiedad siempre se cumple (aunque la comprobemos en muchos casos particulares).
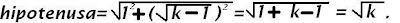
No hay comentarios:
Publicar un comentario